GeoClassroom Physical Geology Historical Geology Structure Lab Mineralogy Petrology

Tectosilicates


Feldspars

What you must learn

  • Solid solution between albite and anorthite (plagioclase series).
  • High temperature solid solution between KAlSi3O8 (sanidine) and NaAlSi3O8 (albite).
  • High-temperature disorder of Al and Si on tetrahedral sites (sanidine vs. microcline).

Structure, Crystal Chemistry and Compositions of Feldspars

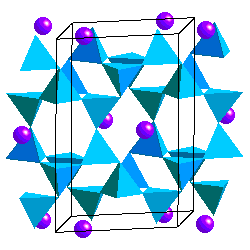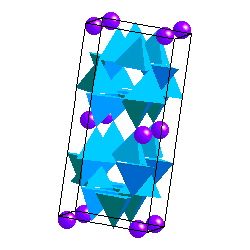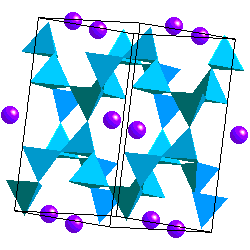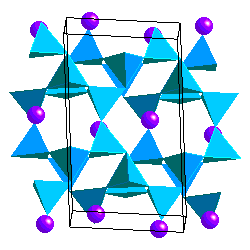
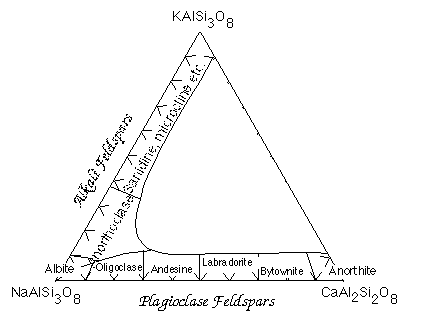
Feldspars are tectosilicates in which each (Al,Si)O4 tetrahdedron is corner-sharing with 4 others. The tetrahedra form four-membered rings Because some of the Si atoms are replaced by Al, there is a net charge on the framework so the structure accomodates K+, Na+ or Ca2+ cations. Ca2+ and Na+ have similar ionic radii. The coupled substitution Ca-Al and Na-Si results in a continuous solid solution between albite (NaAlSi3O8) and anorthite (CaAl2Si2O8). Feldspars of intermediate composition have are called oligoclase, andesine, labradorite and bytownite. However, it is not necessary that you know these. A solid solution between albite and andesite is called plagioclase. The ionic radii of Ca and K are sufficiently different, however, that there is no solid solution between anorthite and KAlSi3O8. On the other hand, the ionic radii of K+ and Na+ are similar enough to allow solid solution at high temperature.


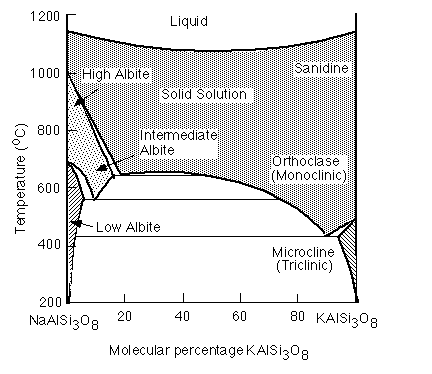
Upon cooling, however, the Na and K endmembers are no longer miscible and the solid solution will exsolve into to feldspars, one Na-rich and the other K-rich. This is another example of a miscibility gap. The exsolution lamellea that result are called perthites .




Al-Si Order-Disorder in Feldspars

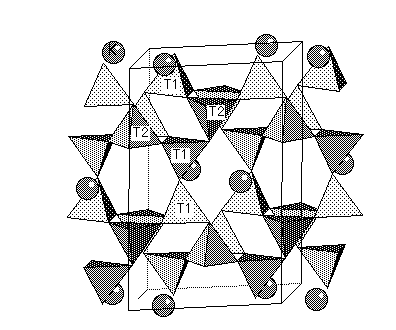
In alkali feldspars, there are two types of tetrahedral sites (T1 and T2) occupied by Al or Si. At high temperatures the Al and Si atoms are disordered over the T1 and T2 sites.

The resulting structure has monoclinic symmetry and is called sanidine . With cooling, the Al and Si atoms order to prevent Al atoms from occupying adjacent tetrahedral sites (the "Al avoidance principle"). The resulting structure is triclinic and called microcline.

Twinning in Feldspars

Sanidine, Microcline and Plagioclase have characteristic twinning which helps distinguish them. Sanidine typically shows the Carlsbad Twin law:
Sanidine in Plane Polarized light Sanidine in Cross-Polarized Light

Microcline shows a characteristic cross hatched twinning that results from the Al-Si ordering upon cooling.
Microcline in Plane Polarized light Microcline in Cross-Polarized Light

Plagioclase shows the characteristic albite twinning that results from the Al-Si ordering upon cooling.
Plagioclase in Plane Polarized light Plagioclase in Cross-Polarized Light

Silica Polymorphs

What you must learn:

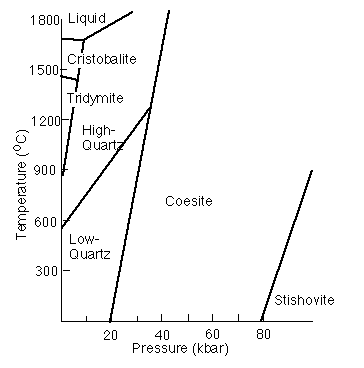
The SiO2 phase diagram

A number of polymorphs of SiO2 exist at high temperature and pressure. These are more stable because they have a higher entropy or density than alpha-quartz.

Here is another way to represent the temperature dependence of the polymorph stabilities. Below is a figure showing the Gibbs Free energy vs. temperature for each low-pressure phase.

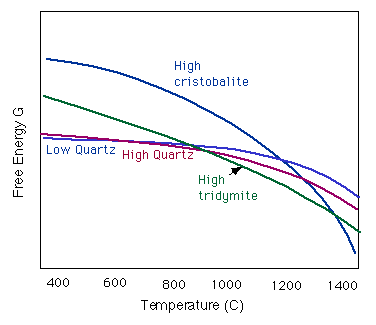
Structures of the SiO2 Polymorphs

Alpha and Beta-quartz

The stable form of SiO2 at low pressure and temperature is alpha-quartz. The SiO4 tetrahedra share corners to form 6-membered rings. The SiO4 tetrahedra share corners to form 6-membered rings.

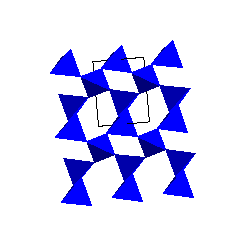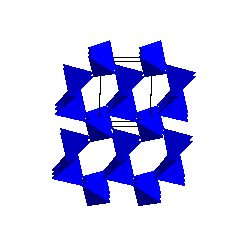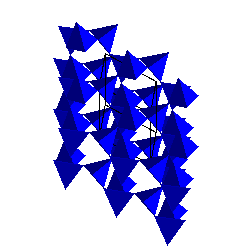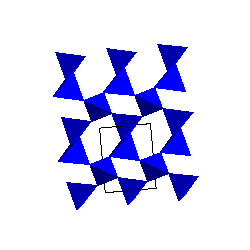Tridymite

The tridymite structure also has 6-membered rings of SiO4 tetrahedra but the resulting symmetry of the structure is higher than that of quartz.

Cristobalite

The cristobalite structure is cubic but the illustration here is on the (111) plane to show the sheets of SiO4 tetrahedra stacked on top of each other. Because cristobalite has the highest symmetry, it also has the highest entropy of the silica polymorphs. Hence, it is stable at the highest temperatures.

Coesite

Coesite is a denser structure that results when the SiO4 tetrahedra link up by forming 4-membered rings. At mantle pressures, the cost in internal energy required to form the 4-membered rings is overcome by the PV term.

Stishovite

Stishovite is the highest-pressure form of SiO2. Here, in the interest of creating the densest structure we can, the Si atoms are in 6-fold coordination and the polyhedra share edges to form the rutile structure.

Symmetry and Entropy revisited

The SiO2 polymorphs give us a useful example of how high-temperature polymorphs will always have a higher symmetry. The reason for this is that high-symmetry structures will have a higher entropy.

Phase Crystal System Space Group Temperature
Alpha Quartz Hexagonal P3221 --
Beta Quartz Hexagonal P6222 574 oC
High Tridymite Hexagonal P63/mmc 870 oC
High Cristobalite Cubic Fd3m 1470 oC

Except for beta quartz, the high temperature polymorphs result from reconstructive phase transitions. Consequently, there is a kinetic barrier to their transformation back to alpha-quartz upon cooling and we might expect to find these phases in rocks that have cooled sufficiently rapidly. One complication, however, that you must be aware of is that both tridymite and cristobalite revert to lower symmetry modifications via a displacive transformation. Consequently, in a thin-section, we will only find low-tridymite (monoclinic or orthorhombic) and low-cristobalite (tetragonal).

All Pages Copyright © GeoClassroom. All Rights Reserved.